Objectif : découvrir la technique des « arbres couvrants », très utilisée en informatique pour résoudre des problèmes de la vie courante
Activité issue de l’ouvrage Unplugged
Il était une fois une ville qui n’avait pas de rues. Il était très difficile de circuler dans la ville après de fortes pluies car le sol était boueux, les voitures s’embourbaient et les bottes des habitants étaient toutes crottées. Le maire de la ville décida de paver certaines rues mais il ne voulait pas dépenser plus que nécessaire car il voulait également faire construire une piscine pour la ville. Le maire spécifia donc deux conditions :
- Paver suffisamment de rues pour que chacun des habitants puisse se rendre de sa maison à n’importe quelle autre maison en empruntant des rues pavées.
- Dépenser le moins d’argent possible pour paver ces rues.
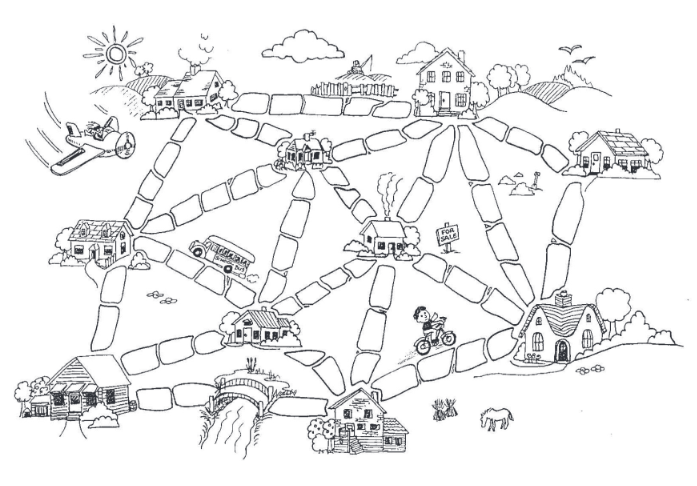
L’agencement de la ville est représenté ci-dessous. Le nombre de pavés entre chaque maison représente la dépense à engager pour paver la route.
Il s’agit de trouver le meilleur chemin pour relier toutes les maisons en utilisant le moins de pavés possible.
Pour effectuer les tests :
- réaliser le parcours dessiné dans la cour
- revenir en classe pour schématiser le parcours
Ce type de problème ne comporte pas de solution unique, des échanges seront menés entre les élèves. Joseph Kruskal, mathématicien américain, en 1956, a proposé un algorithme pour déterminer une solution: l’Algorithme de Kruskal. Il suffit de sélectionner les arêtes par ordre croissant de leur longueur. On commence par les plus petites et on complète petit à petit, en gardant à l’esprit que le nombre optimal d’arêtes est égal au nombre de nœuds moins un.