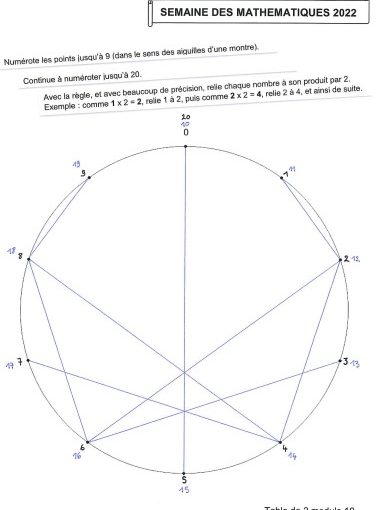
Propositions de réalisations pour la classe
1- Réaliser la représentation graphique de tout autre nombre supérieur à 9.
Dans cette perspective, il est conseillé d’inscrire autour du cercle uniquement les nombres de 0 à 36 (si 36 points sur le cercle sont choisis) et les multiples de la table que l’on souhaite représenter.
Les élèves doivent alors résoudre le problème : Comment trouver la place d’un nombre (multiple de la table choisie) sur le cercle modulo 36 sans écrire la suite des nombres ?
Ils s’appuieront sur les observations de l’étape 3 pour en déduire que ce nombre peut s’écrire sous la forme d’un multiple de 36 auquel on ajoute un nombre compris entre 1 et 35.
Une stratégie consiste alors à chercher le plus proche multiple de 36 inférieur au nombre dont on cherche la place sur le cercle, et de poursuivre la numérotation des points sur le cercle, à partir de 0 jusqu’au nombre désiré.
Une autre stratégie de calcul consiste à chercher le plus proche multiple de 36 inférieur au nombre dont on cherche la place sur le cercle, et de le soustraire au nombre dont on cherche la place. Le résultat indique la place sur le cercle.
Par exemple, si je cherche la place de 78 (6×13) sur le cercle modulo 36, après avoir listé les multiples de 36, je soustraie 72 (2×36) à 78, j’obtiens 4 C’est la place du nombre 72 sur le cercle modulo 36. 4 et 72 occupent la même place sur le cercle car 78 = (2×36) + 4
Une autre stratégie de calcul, qui traduit la précédente stratégie, consiste à réaliser la division euclidienne du nombre (dont on cherche la place sur le cercle) par 36. Le reste de cette division indiquant la place sur le cercle.78 : 36 = 2 avec un reste de 4
Certaines tables permettent d’obtenir des motifs intéressants comme la table de 31 modulo 48 ou 55 modulo 84 qui donnent à voir un réseau de triangles, 17 modulo 36 ou 41 modulo 84 qui donnent à voir un réseau de rectangles, 23 modulo 36, etc.
2 – Réaliser la représentation graphique de tout autre nombre décimal, puis visualiser la vidéo de 5 min 56 à 7 min 10, en observant la légende de chaque table qui s’affiche. Attention, les tables de nombres décimaux à plusieurs décimales sont trop complexes à représenter avec le papier et le crayon, se contenter de nombres à une seule décimale.
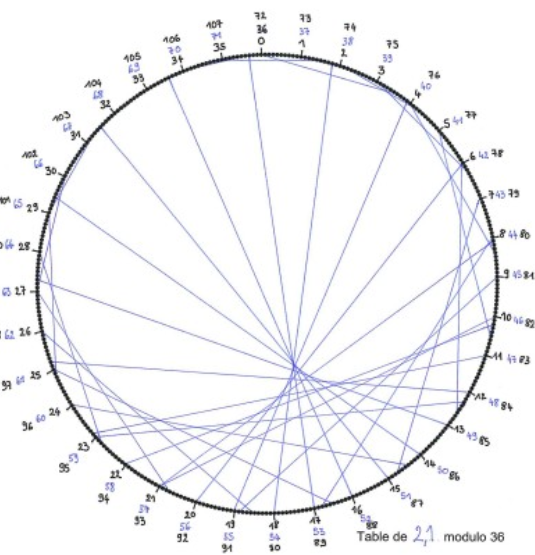
3 – Réaliser une représentation de la table d’un nombre sur un cercle comprenant plus ou moins de points. Attention, plus il y a de points sur le cercle, plus les calculs sont nombreux et plus les tracés demandent de la précision.
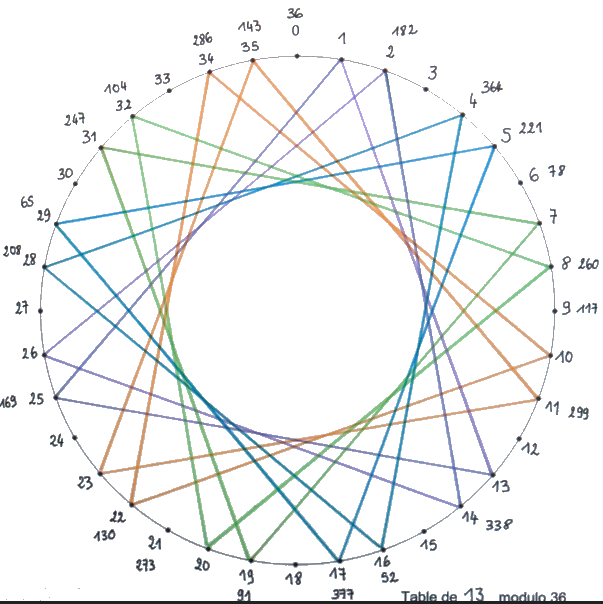
4 – Observer et décrire des représentations. Par exemple la table de 13 modulo 36 donne à voir des triangles équilatéraux.
Différents gabarits de cercles, avec plus ou moins de points, sont disponibles en téléchargement :
eleve_etape_7_modulo_12eleve_etape_7_modulo_24
eleve_etape_7_modulo_48
eleve_etape_7_nombre_decimal_modulo36